Как быть, если вы столкнулись с погрешностью межевания земельного участка: каков её допустимый показатель?
Содержание:
Оценка погрешности при прямых измерениях
При прямых измерениях искомая величина определяется непосредственно по отсчетному устройству (шкале) средства измерения. В общем случае измерения проводятся по определённому методу и при помощи некоторых средств измерений. Эти компоненты несовершенны и вносят свой вклад в погрешность измерения. Если тем или иным путём погрешность измерения (с конкретным знаком) удаётся найти, то она представляет собой поправку, которую просто исключают из результата. Однако достичь абсолютно точного результата измерения невозможно, и всегда остаётся некоторая «неопределённость», которую можно обозначить оценив границы погрешности.
В зависимости от имеющихся исходных данных и свойств оцениваемых погрешностей используют различные способы оценки. Случайная погрешность, как правило, подчиняется закону нормального распределения для описания которого необходимо указать математическое ожидание M и среднеквадратическое отклонение σ. В связи с тем, что при измерении проводится ограниченное число наблюдений, находят только наилучшие оценки этих величин: среднее арифметическое результатов наблюдений x¯{\displaystyle {\bar {x}}} и среднеквадратическое отклонение среднего арифметического Sx¯{\displaystyle S_{\bar {x}}}:
x¯=∑i=1nxin{\displaystyle {\bar {x}}={\frac {\sum _{i=1}^{n}x_{i}}{n}}}; Sx¯=∑i=1n(xi−x¯)2n(n−1){\displaystyle S_{\bar {x}}={\sqrt {\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}{n(n-1)}}}}
Доверительные границы ε полученной таким образом оценки погрешности определяются умножением среднеквадратического отклонения на коэффициент Стьюдента t, выбранный для заданной доверительной вероятности P:
ε=tSx¯{\displaystyle \varepsilon =tS_{\bar {x}}}.
Систематические погрешности в силу своего определения не могут быть оценены путем проведения многократных измерений. Для составляющих систематической погрешности, обусловленной несовершенством средств измерений, как правило известны только их границы, представленные, например, основной погрешностью средства измерения.
Итоговая оценка границ погрешности получается суммированием вышеприведённых «элементарных» составляющих, которые рассматриваются как случайные величины. Эта задача может быть математически решена при известных функциях распределений этих случайных величин. Однако, в случае систематической погрешности, такая функция как правило неизвестна и форму распределения этой погрешности задают как равномерную. Основная трудность заключается в необходимости построения многомерного закона распределения суммы погрешностей, что практически невозможно уже при 3—4 составляющих. Поэтому используются приближённые формулы.
Суммарную неисключённую систематическую погрешность, когда она состоит из нескольких m компонентов, определяют по следующим формулам:
Θ∑=±∑i=1m|Θi|{\displaystyle \Theta _{\sum }=\pm \sum _{i=1}^{m}\left|\Theta _{i}\right|} (если m<3{\displaystyle m<3});
Θ∑(P)=±∑i=1mΘi2{\displaystyle \Theta _{\sum }(P)=\pm {\sqrt {\sum _{i=1}^{m}\Theta _{i}^{2}}}} (если m⩾3{\displaystyle m\geqslant 3}),
где коэффициент k для доверительной вероятности P=0,95 равен 1,1.
Суммарная погрешность измерения, определяемая случайной и систематической составляющей, оценивается как:
Δ=KSx¯2+Θ∑23{\displaystyle \Delta =K{\sqrt {S_{\bar {x}}^{2}+{\frac {\Theta _{\sum }^{2}}{3}}}}} или Δ=KSx¯2+(Θ∑(P)k3)2{\displaystyle \Delta =K{\sqrt {S_{\bar {x}}^{2}+\left({\frac {\Theta _{\sum }(P)}{k{\sqrt {3}}}}\right)^{2}}}},
где
K=ε+Θ∑Sx¯+Θ∑3{\displaystyle K={\frac {\varepsilon +\Theta _{\sum }}{S_{\bar {x}}+{\frac {\Theta _{\sum }}{\sqrt {3}}}}}} или K=ε+Θ∑(P)Sx¯+Θ∑(P)k3{\displaystyle K={\frac {\varepsilon +\Theta _{\sum }(P)}{S_{\bar {x}}+{\frac {\Theta _{\sum }(P)}{k{\sqrt {3}}}}}}}
Окончательный результат измерения записывается какA±Δ(P){\displaystyle A\pm \Delta (P)}, где A — результат измерения (x¯{\displaystyle {\bar {x}}}), Δ{\displaystyle \Delta } — доверительные границы суммарной погрешности, P — доверительная вероятность.
Точность и погрешность
При проведении измерительных

работ важными показателями являются точность измерений и их погрешность.
Измерительные системы не могут определить абсолютно достоверно измеряемые величины, что связано с некоторыми допустимыми отклонениями и помехами. Это приводит к какой-то неточности.
Неточность измерений характеризуется:
- погрешностью – разностью между истинным и измеренным значениями;
- точностью – случайным разбросом ошибок около их средней величины.
В процессе межевания для оценки точности координат характерных точек рассчитывается средняя квадратическая погрешность (СКП):
Mt – СКП расположения характерной точки по отношению к пункту ОМС;
m0 – СКП положения точки съемки по отношению к пункту ОМС;
m1 – СКП расположения характерной точки относительно точки съемки, с которой производилось определение координат характерной точки.

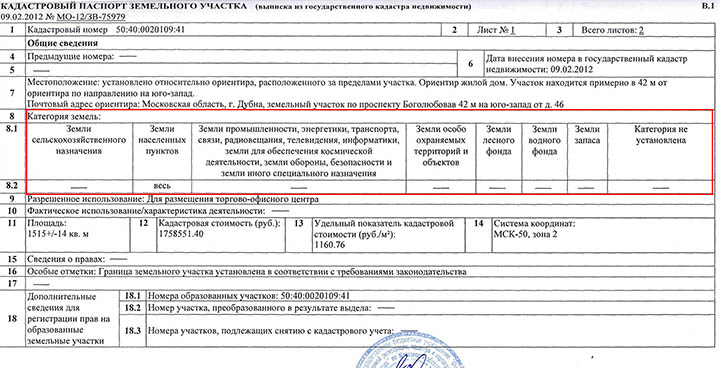
Допустимая точность межевания ЗУ задано нормативно (Приложение к Приказу МЭР № 518). Она зависит от типа земель, на которых производится межевание ЗУ.
В соответствии с документацией СКП для населенных пунктов составляет 10 см, для с/х земель – 250 см, причем для дачных и садоводческих участков эта погрешность не должна превышать 20 см. Самые большие допуска обозначены для лесного и водного фонда – 5 м.
При проведении межевания площадь ЗУ определяется с учетом координат поворотных точек.
При этом абсолютное значение разности вычисленной по координатам площади (Рвыч) и площади ЗУ (Рдок), указанной в документе на участок, не должно превышать допустимую величину ΔРдоп:
- ΔР=|Рвыч-Рдок| ≤ ΔРдоп, где
- ΔРдоп= 3,5 Mt √(Рдок), м2
При выполнении этого условия в качестве основной величины принимается Рвыч. Если ΔР > ΔРдоп, то исполнитель работ должен провести анализ причин этого превышения и написать заключение.
Классификация погрешностей измерений
По способу выражения
- Абсолютная погрешность
- Абсолютной называют погрешность, выраженную в единицах измеряемой величины. Её можно описать формулой ΔX=Xизм−Xист{\displaystyle \Delta X=X_{\text{изм}}-X_{\text{ист}}}. Вместо истинного значения измеряемой величины, на практике пользуются действительным значением Xд{\displaystyle {X_{\text{д}}}}, которое достаточно близко к истинному, определяется экспериментальным путем и в конкретной задаче может приниматься вместо него. Из-за того что истинное значение величины всегда неизвестно, можно лишь оценить границы, в которых лежит погрешность, с некоторой вероятностью. Такая оценка выполняется методами математической статистики.
- Относительная погрешность
- Относительная погрешность выражается отношением δX=ΔXXд{\displaystyle \delta X={\frac {\Delta X}{X_{\text{д}}}}}. Относительная погрешность является безразмерной величиной; её численное значение может указываться, например, в процентах.
По источнику возникновения
- Инструментальная погрешность
- Эта погрешность определяется несовершенством прибора, возникающим, например, вследствие расхождения его реальной функции преобразования от калибровочной зависимости.
- Методическая погрешность
- Методической называют погрешность, обусловленную несовершенством метода измерений. К таким можно отнести погрешности от неадекватности принятой модели объекта от реального объекта или от неточности расчётных формул.
- Субъективная погрешность
- Субъективной является погрешность, обусловленная ограничениями человека, как оператора при проведении измерений. Проявляется, например, в неточностях при отсчете показаний со шкалы прибора.
По характеру проявления
- Случайная погрешность
- Это составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их влияние обычно можно устранить статистической обработкой. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.
Математически случайную погрешность, как правило, можно представить белым шумом: как непрерывную случайную величину, симметричную относительно нуля, независимо реализующуюся в каждом измерении (некоррелированную по времени).
Основным свойством случайной погрешности является возможность уменьшения искажения искомой величины путём усреднения данных. Уточнение оценки искомой величины при увеличении количества измерений (повторных экспериментов) означает, что среднее случайной погрешности при увеличении объёма данных стремится к 0 (закон больших чисел).
Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине часто полагают распределение случайной погрешности «нормальным» (см. Центральная предельная теорема). «Нормальность» позволяет использовать в обработке данных весь арсенал математической статистики.
Однако априорная убежденность в «нормальности» на основании Центральной предельной теоремы не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.
Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).
- Систематическая погрешность
- Это погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.
Систематическую ошибку нельзя устранить повторными измерениями. Её устраняют либо с помощью поправок, либо «улучшением» эксперимента.
Деление погрешностей на случайные и систематические достаточно условно. Например, ошибка округления при определённых условиях может носить характер как случайной, так и систематической ошибки.
Допуск
На производстве используют понятие допуск, устанавливая верхнее и нижнее значение, в пределах которых
измеряемый объект не считается браком. Например, при производстве конденсаторов ёмкостью 100±5% мкФ
устанавливается допуск 5%, это означает, что на этапе контроля качества при замере ёмкости конденсатора,
конденсаторы ёмкостью более 105 мкФ и менее 95 мкФ считаются браком.
При контроле качества необходимо учитывать неопределённость измерительного инструмента, так, если
неопределённость измерения ёмкости конденсатора составляет 2 мкФ, то результат измерения 95 мкФ может
означать 93-97 мкФ. Для учёта неопределённости в результатах измерений необходимо расширить
понятие допуска: в допуске должна быть учтена неопределённость измерительного прибора. Для этого необходимо
задать доверительный интервал, т.е. процент деталей, который должен гарантированно соответствовать заданным
параметрам.
Доверительный интервал строится по нормальному распределению: считается, что результат измерения
соответствует нормальному распределению
μ±kσ. Вероятность нахождения значения в пределах ku зависит от значения k:
при k=1 68,3% измерений попадут в значение σ±u, при k=3 — 99,7%.
Шаги
Часть 1 из 3:
Среднее значение
-
1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.
X
Источник информации- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-
2
Для вычисления среднего значения понадобятся все числа данного набора данных.
X
Источник информации- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-
3
Сложите все числа вашего набора данных.
X
Источник информации- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.
X
Источник информации- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Часть 2 из 3:
Дисперсия
1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.
X
Источник информации
Эта величина даст вам представление о том, как разбросаны данные выборки.
Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.
X
Источник информации
В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
Проделайте вычитания еще раз, чтобы проверить каждый ответ
Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.
X
Источник информации
При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.
X
Источник информации
В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
4 + 0 + 4 + 0 + 0 + 16 = 24.
Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке
Таким образом, вы получите дисперсию.
X
Источник информации
В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
n-1 = 5.
В нашем примере сумма квадратов равна 24.
24/5 = 4,8
Дисперсия данной выборки равна 4,8.
Часть 3 из 3:
Среднеквадратическое отклонение
-
1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.
X
Источник информации- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.
X
Источник информации- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.
X
Источник информации- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
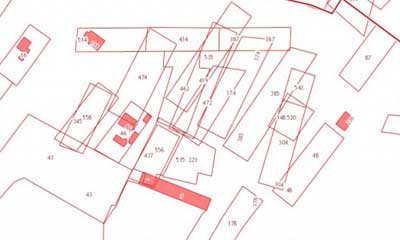
Поворотные точки
У земельного участка должны быть определённая конфигурация, простая или сложная. Вовсе не всегда участок представляет собой квадрат или прямоугольник с углами по 90 градусов – во многих случаях эти углы могут быть другими, что делает измерения сложнее. Все места, в которых направление меняется, необходимо зафиксировать – они и будут называться поворотными точками.
На межевом плане их легко выделить, и именно по ним определяется положение участка, а его границы проводятся от точки до точки. От их количества зависит стоимость межевания, а значит, чем проще участок по форме, тем дешевле проведение его межевания. Ведь чтобы измерить простой четырёхугольник, потребуются лишь 4 поворотные точки, а если форма участка сложнее, и он имеет изгибы, то и число точек для измерения возрастает с каждым следующим всё больше.
Метрологическая лаборатория
Лаборатория метрологии должна контролировать все косвенные факторы измерения. Условия зависят от типа и точности
измерений. Так, лабораторией может считаться даже отдел измерений на производстве. Ниже будет рассказано об
основных требованиях к метрологической лаборатории.
Расположение
Метрологическая лаборатория должна быть расположена максимально удалённо от других зданий, находится
на самом низком этаже (лучше — в подвале) и обладать достаточной изоляцией от шума, перепада температур,
вибраций и других источников раздражения.
Температура
В метрологической лаборатории должен соблюдаться температурный режим, который учитывает находящихся
в лаборатории сотрудников. Необходимо наличие системы кондиционирования воздуха и отопления.
Освещение
Освещение должно производиться люминесцентными лампами холодного цвета, освещённость должна составлять от 800 до 1000 лк.
Что такое дисперсия
Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.
Чтобы найти дисперсию последовательно проведите следующие вычисления:
- Определите среднее (простое среднее арифметическое ряда значений).
- Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
- Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).
Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.
| Порода собаки | Рост в миллиметрах |
| Ротвейлер | 600 |
| Бульдог | 470 |
| Такса | 170 |
| Пудель | 430 |
| Мопс | 300 |
Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.
Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:
Среднее мм.
Итак, среднее (среднеарифметическое) составляет 394 мм.
Теперь нужно определить отклонение роста каждой из собак от среднего:
Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:
Дисперсия мм2.
Таким образом, дисперсия составляет 21704 мм2.
Как найти среднеквадратическое отклонение
Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:
мм (округлено до ближайшего целого значения в мм).
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).
Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.
То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.
Неопределённость измерительного инструмента
Неопределённость может быть определена посредством сравнения результатов замеров с образцом
или замером инструментом более высокой точности. В процессе калибровки инструмента выводится
корректировочное значение и неопределённость.
Пример калибровки микрометра
Замерив образец заранее известной длины, мы получим значение корректировки, c. Таким образом, если длина, измеренная
инструментом равна x, фактическая длина будет равна xc = x + c.
Произведём nc замеров образца и получим отклонение sc. Теперь, при любых замерах
откалиброванным микрометром, значение неопределённости u будет равно:
u = √(u2 + s2c/nc + u2m/n),
um — отклонение полученное при n замерах.